Laminar flow around a 2D cylinder – Kármán vortex shedding
Low Reynolds number flows around a cylinder is one of the most well-known, and most investigated cases in Computational Fluid Dynamics (CFD). It is probably due to the interesting phenomenon that can occur in this type of flow, the Karman vortex shredding.
Around Re 90-150 the fluid behind the cylinder starts to produce vortexes with periodically opposite orientations. The phenomenon became a great benchmark and validation case, considering the simplicity of the geometry combined with the complex behaviour of the flow.
The purpose of this study is to investigate the effect of different meshing methods on the solution accuracy.
The lift- (CL) and drag coefficients (CD) were investigated on a 2D cylinder using OpenFOAM. Since these are time dependent – oscillating values, an average was calculated for the drag- and a root mean square for the lift coefficient using the following formulas:
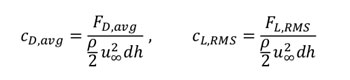
Flow with four different Re numbers (from 90-150) was examined. The investigations of Henderson and Norberg were considered as the target, the reference data is summarised in the table below.
Table 1. Experimental data for the cylindrical bodies

Air was used in the analyses, in order to accurately recreate the experimental environment. To maintain low Re numbers. we had to set our inlet velocity ranging from 0.0073 m/s to 0.022 m/s. The length of the wind tunnel was 10 meters, and the height was 8 meters. The model setup is displayed in the following sketch.

Figure 1. Model setup.
Since the simulation was laminar and transient, OpenFOAM’s icoFoam solver was used for the analysis. The initial mesh was generated with Salome Meca’s Netgen module. The prism-dominant (extruded triangles) mesh with the use of viscous sublayers consisted of 81 000 cells and can be seen in the pictures below.

Figure 2. CFD mesh generated by Salome Meca’s Netgen module consisting of 81 000 cells.
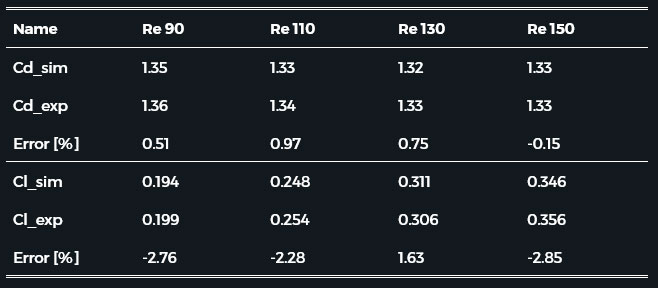
Table 2. summarises the simulation result lift- (CL) and drag coefficients (CD) compared with the experimental results. The simulation results seem accurate based on the comparison.
Table 2. Lift- and drag coefficient around a 2D cylinder at Re 90-150.
The following animation shows the laminar vortex shedding at Re = 150:
A further mesh convergence study was made, to find more efficient approaches to solve this problem.
Fully hexahedral meshes were investigated generated by OpenFOAM’s blockMesh utility. Four refinement levels were made, both with Salome and blockMesh. These meshes are displayed in the following Figures.
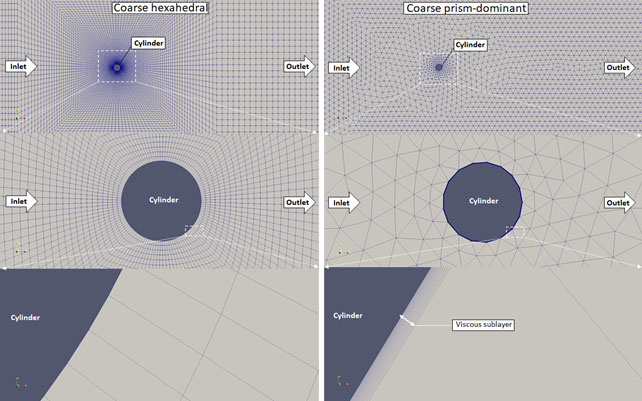
Figure 3. Coarse meshes generated with snappyHexMesh (left) and Salome Meca (right)
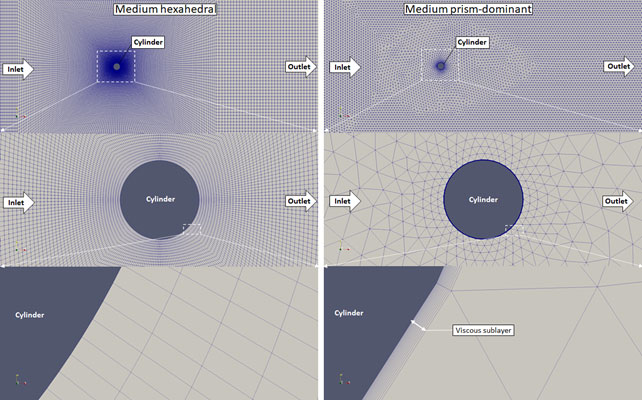
Figure 4. Medium meshes generated with snappyHexMesh (left) and Salome Meca (right)
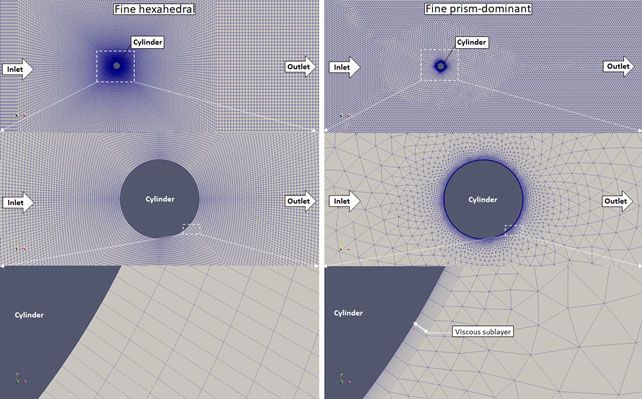
Figure 5. Fine meshes generated with snappyHexMesh (left) and Salome Meca (right)
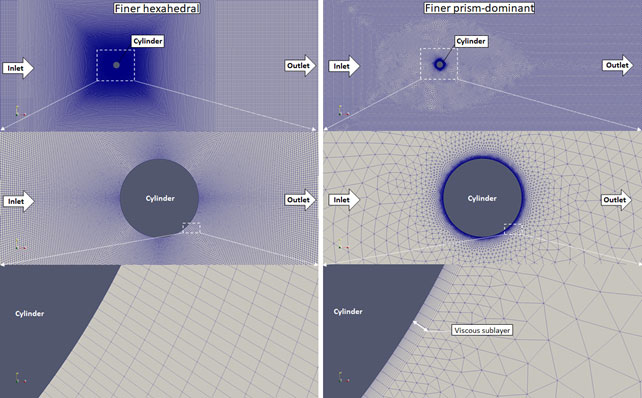
Figure 6. Finer meshes generated with snappyHexMesh (left) and Salome Meca (right)
The meshes displayed in Fig. 3-6. were used to run the scenario at a Reynolds number of 150. For these simulations the wind tunnel height was decreased to 3 meters, because it seemed to be perfectly enough for the flow to develop undisturbedly. The Salome generated meshes were labelled with “sm” initials whereas the blockMesh generated ones got the “bm” label.
An animation of the vortex shredding forming in each case.
And also diagrams of the lift- (CL) and drag coefficients (CD) in each timestep, on the coarse and finer prism-mesh.
Drag coefficient (CL) in a coarse and finer prism-dominant mesh
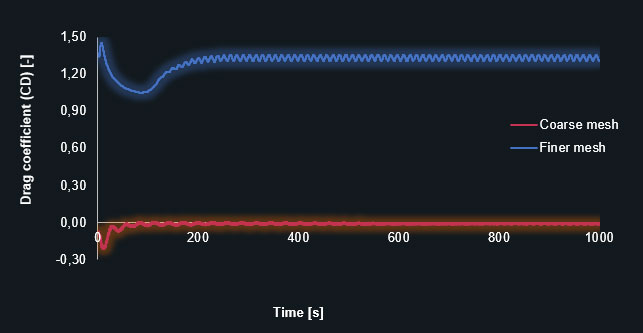
Drag coefficient (CD) – coarse prism-dominant mesh
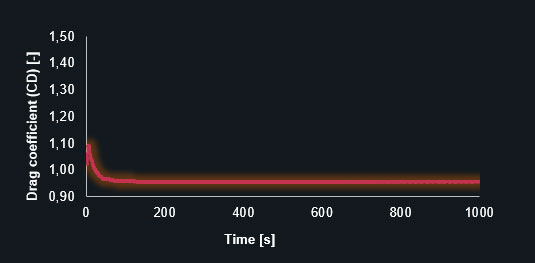
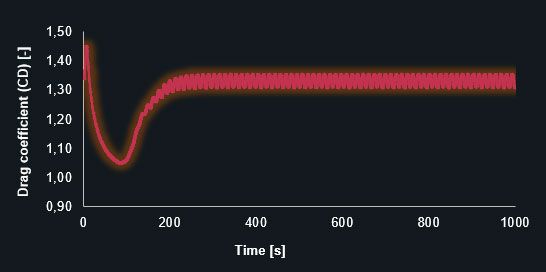
Drag coefficient (CD) – fine prism-dominant mesh
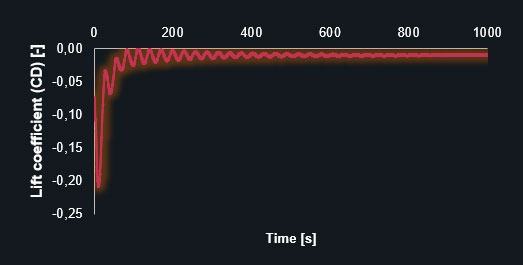
Lift coefficient (CL) – coarse prism-dominant mesh
Lift coefficient (CL) – fine prism-dominant mesh
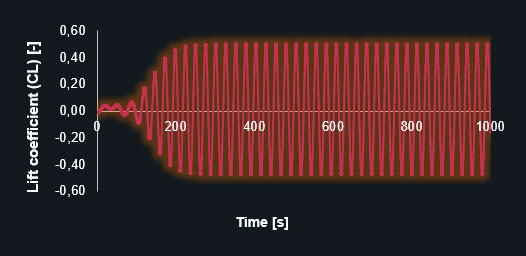
The diagrams clearly show that the finer mesh produces the expected oscillating results for the lift and drag coefficients. The simulation with the coarse mesh converges to a discrete value leading to an inaccurate solution. The following table contains the results in detail.
Table 3. Comparison of the different meshing methods at different refinement levels
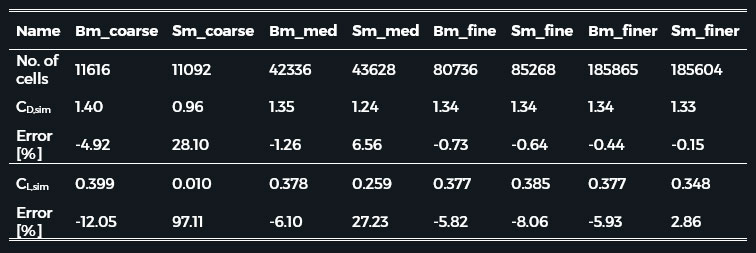
As the results show the hexahedral mesh can produce more accurate results with the same number of cells. But nevertheless, at the end, the Salome prism-dominant mesh gave the best result. This is probably due to the added viscous sublayers and the considerably finer mesh around the cylinder.
The animation also shows that the prism meshes that converged, converged much faster than the hexahedral ones. (Although the simulation with the coarse mesh didn’t even started the vortex shedding.)
Generally speaking, a blockMesh generated mesh leads to precise and fast results. In case one needs even more precision, it is worth using a finer mesh and viscous sublayers.






