Tesla szelep – állandó geometriájú, „visszacsapó” szelep
2022.04.14.
A Tesla szelep, egy állandó geometriájú passzív “visszacsapó” szelep, amely azt jelenti, hogy a szelep nem tartalmaz mozgóalkatrészt, ebből adódóan a szelep működését csak a geometriája határozza meg.
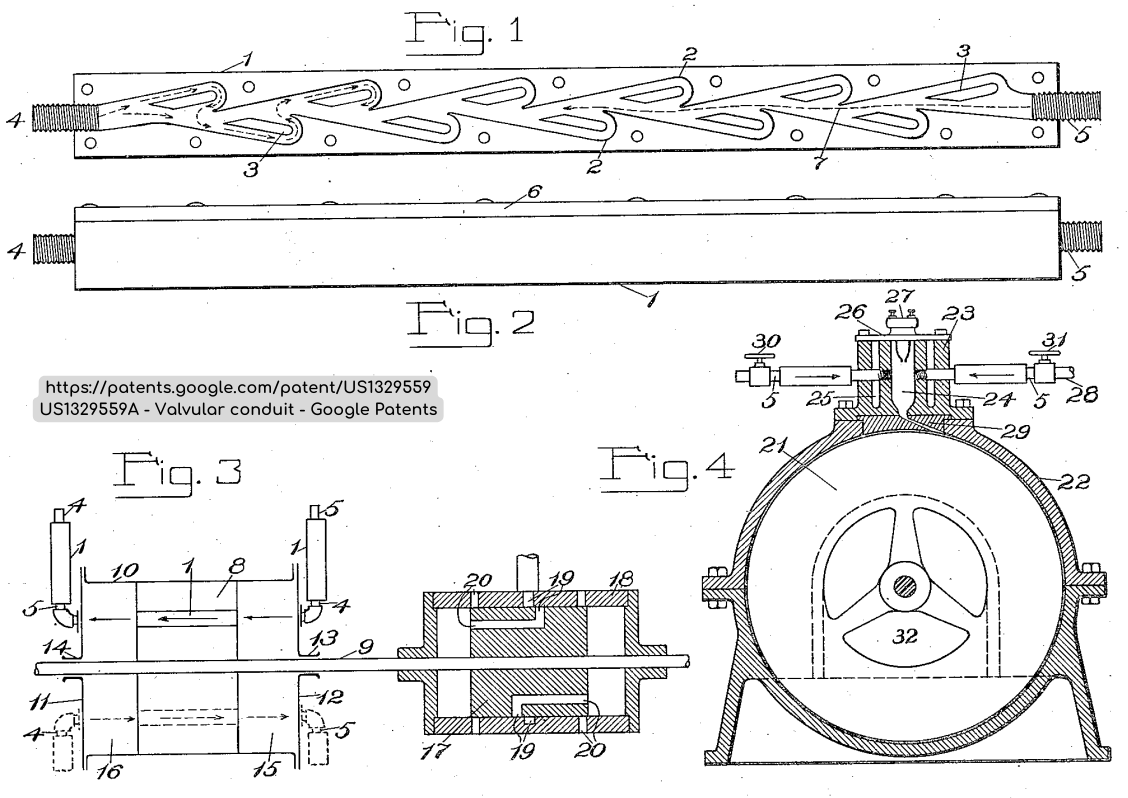
Nikola Tesla, a szelep feltalálója, eredeti publikációjában mutatta be az általa létrehozott szelep geometriáját, amely az alábbi ábrán látható.

1. ábra: Tesla szelep eredeti geometriája.
Az előre haladó áramlás (5) során a közeg a szelep főágban haladó áramlását a mellékágakban történő áramlás nem akadályozza meg, a létrejövő nyomásesést csak a közeg belső súrlódása hozza létre. Ezzel szemben az ellentétes irányú áramlás (4) esetén a főágban haladó áramlást, a mellékágakból visszafolyó közeg akadályozza, amely további nyomásesést hoz létre a be- és kiáramlási keresztmetszetnél mérhető nyomás között.
A szelep fő jellemzője a diodicitás, amely az ellentétes irányú áramlás során létrejövő nyomásesés (Δpr) és az előre haladó áramlás során létrejövő nyomásesés (Δpf) hányadosa, állandó térfogatáramok esetén.
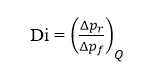
A Tesla szelepre jellemző diodicitás vizsgálata során a beáramlási keresztmetszetre normál irányú sebességkomponens értékét állandónak feltételeztük, valamint az áramlás lamináris, illetve turbulens viselkedésének megfigyelése érdekében a beáramlási sebességet, az áramlásra jellemző Reynolds-szám alapján határoztuk meg.
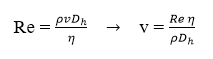
A beáramló közeg sebességének meghatározása során az áramló közeget víznek vettük, így annak megfelelően határoztuk meg az áramló közeg sűrűségét (), valamint a dinamikai viszkozitását (). A beáramlási keresztmetszet téglalap alakú, így egy hidraulikus átmérőt (Dh) kellett meghatározni. Az előző együtthatók meghatározása után kiszámítottuk, a Reynolds-számokhoz tartozó áramlási sebességeket, amely az alábbi táblázatban látható.

1. táblázat: Reynolds-számokhoz tartozó beáramlási sebesség értékek.
Az alábbi animáción az előre haladó és ellentétes irányú áramlás látható, valamint a létrejövő relatív nyomás értékének változása a légköri nyomáshoz képest a szelep hossza mentén. Az animáción a beáramló közeg sebessége a Re 2000-hez tartozó érték.
Megfigyelhető, hogy ellentétes irányú áramlás esetén az áramló közeg kezdetben lamináris viselkedést mutat, mindaddig, amíg a főágban áramló közeg találkozik a mellékágból kiáramló közeggel, amely hatására turbulens áramlások alakulnak ki. Ezzel szemben az előre haladó áramlás esetén a mellékágban történő áramlás nem befolyásolja a főág áramlását, a létrejövő relatív nyomás értékét csak az közeg belső súrlódásából adódik.
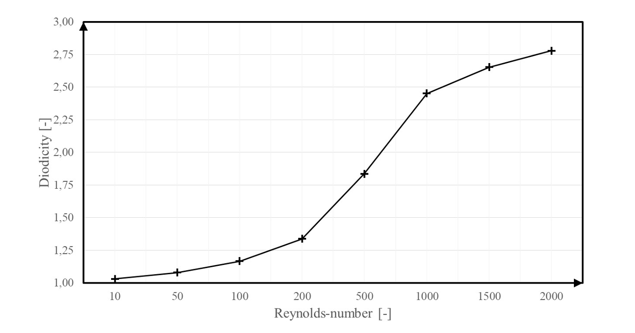
2. ábra: Reynolds-számokhoz tartozó diodicitás értékek.
Alacsony Reynolds-számok esetén a különböző áramlási irányokhoz tartozó relatív nyomás értéke kis eltérést mutat, azaz a diodicitás értéke 1-hez közeli. A Reynolds-szám növelésével az eltérés mértéke növekszik, amely azt eredményezi, hogy a diodicitás értéke is megnő.
A kapott eredmények alapján belátható, hogy a Tesla szelep alkalmazható visszacsapó szelepként, illetve magas Reynolds-számmal rendelkező áramlások esetén fejti ki leginkább a hatását.
Számítási módszerek validációja – NAFEMS benckmark megoldása code_aster-rel

2022.03.20.
Új végeselemes szoftverekkel történő ismerkedés során előre definiált számítási feladatok elvégzése a validáció egyszerű eszköze. Jelen bejegyzés összefoglal egy ilyen validációs folyamatot, mely egy nyílt forráskódú végeselemes környezetnek, a code_aster-nek (Salome Meca-n keresztüli futtatás) a vizsgálatára irányul.
A mintapélda (The Standard NAFMES Benchmarks: Hemisphere – Point Load, NAFEMS Ltd.) egy 10 [m] sugarú középfelületű, 0.04 [m] falvastagságú gömbhéjat vizsgál, mely egyidejűleg van húzásnak és nyomásnak kitéve (1. ábra). A terhelések 2 [kN]-os koncentrált erőkként kerülnek felvételre az 1. ábra szerint. A peremfeltételek és a geometria szimmetriáját kihasználva negyedmodell alkalmazható a jelenség vizsgálatára.
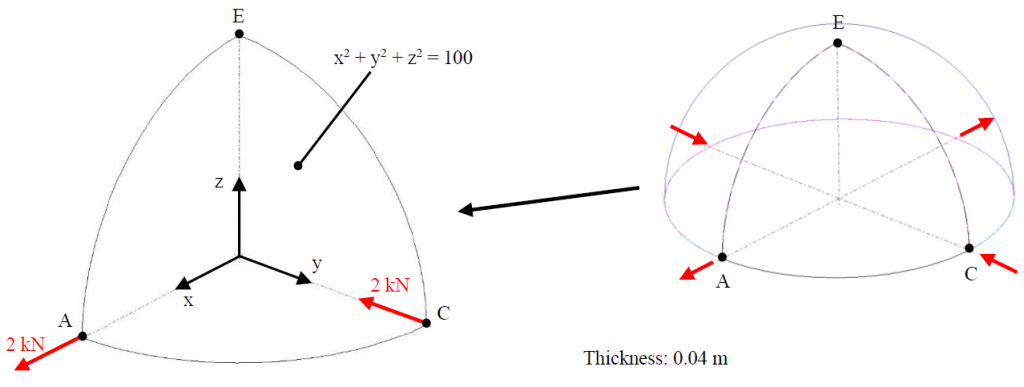
1. ábra – a feladat és a modell.
Morley és Morris elmélete (Morley, L.S.D., Morris, A.J. – Conflict Between Finite Elements and Shell Theory, Kiadvány: 2nd World Congress on Finite Elements: Finite Elements in the Commercial Environment, 532-561. oldal, 1978.) szerint az alábbi, membrán effektust, hajlítást és az élek hatását is figyelembe vevő összefüggéssel írható le a sugár irányú elmozdulás:
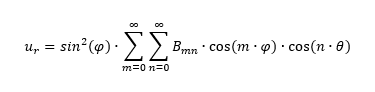
ahol θ a függőleges tengely körüli elfordulást, φ pedig a félgömb tengelyéhez képest sugárirányban mért szög. A Bmn-ek konstansok. Az adott paraméterek mellett az A pont sugár irányú elmozdulása:
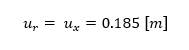
mely megadja a referencia értéket.
A terhelések mellett egyéb peremfeltételek definiálása is szükséges. Az E pont z irányú elmozdulása nulla, illetve szimmetria peremfeltételek hatnak az AE és CE éleken. Az alkalmazott anyagmodell izotropikus, E = 68.25∙103 [MPa], ν = 0.3 [-]. Héjelemek kerültek definiálásra a számításhoz.
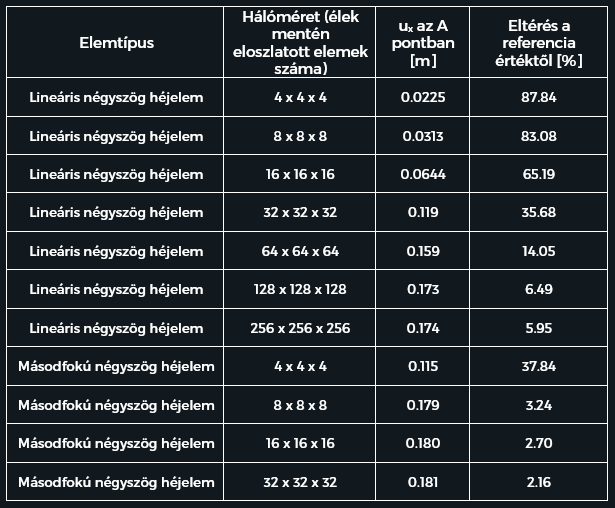
Az 1. táblázat összefoglalja a különböző elemméretű hálókkal készült számítások eredményeit. A hálóméret az egyes élek mentén egyenletesen eloszlatott elemek számát jelenti. Egy elmozdulás mező látható a 2 ábrán.
1. táblázat – a számítási eredmények.
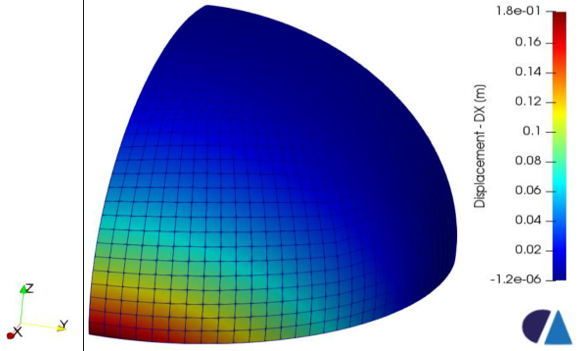
2. ábra – x irányú elmozdulás mező (másodfokú négyszög héjelem, 32 x 32 x 32).
A következő animáció összefoglalja a feladat alapvető információit, valamint a deformált alakkal kibővített elmozdulásmezőt.
A fent részletezett folyamat egy kitűnő lehetőség a nyílt forráskódú megoldások lehetőségeinek kutatására. Amennyiben erőfeszítéseink sikerrel zárulnak, lehetőségünk nyílik olcsóbb, de nem kevésbé szakszerű megoldásokat kínálni partnereink számára.
A VDI2230 méretezési útmutató

2021.06.16.
Aki méretezett már csavart az jó eséllyel szemben találta magát a VDI-vel (fau-dé-i, ha korrekten szeretnénk élő szóban használni), ami nem más, mint a német mérnökök egyesülete (Verein Deutscher Ingenieure) és az általuk kiadott csavarkötésekre vonatkozó méretezési iránymutatás a VDI2230. Nem csak élvezetes olvasmány, de érdemes venni a fáradtságot és végigszámolni egy-egy mintapéldát. Mi megtettük egy robbanómotor hajtókar példáját használva, sőt a számításokat párhuzamosan végeselemes módszerrel is elvégeztük, mert kíváncsiak voltunk hogyan korrelálnak egymással a szimulációs és az analitikus eredmények. Azt tapasztaltuk, hogy az egyszerűsítésekkel élő analitikus leírás a lényegi pontokat tekintve meglepően jól működik a vizsgált csavarkötés viszonylag bonyolult geometriája esetén is. A csavarkötés előfeszítésének sátordiagramjai és az előfeszítésben a külső terhelés hatására létrejövő változást ábrázoló diagramok az analitikus és a numerikus módszerek szerint szinte együtt futnak. A sátordiagramról itt olvasható a blogbejegyzésünk. Érdemes megjegyezni, hogy a csavarkötés kifáradásának szempontjából kulcsfontosságú az az amplitúdó, amit a ciklikusan ható külső terhelő okoz. Habár a sátordiagramon úgy tűnik szinte azonos a FEM és az analitikus eredmény, a kifáradást jellemző amplitúdóban közel 100%-os eltérést tapasztalunk a szimuláció és papíron történő számítások között. Kísérletsorozat eredményeire alapozva lehetne állást foglalni, hogy melyik módszer ad megbízhatóbb becslést. A mérnöki sejtés azt sugallja, hogy a kevesebb elhanyagolással élő szimuláció eredménye lehet közelebb a gyakorlathoz.
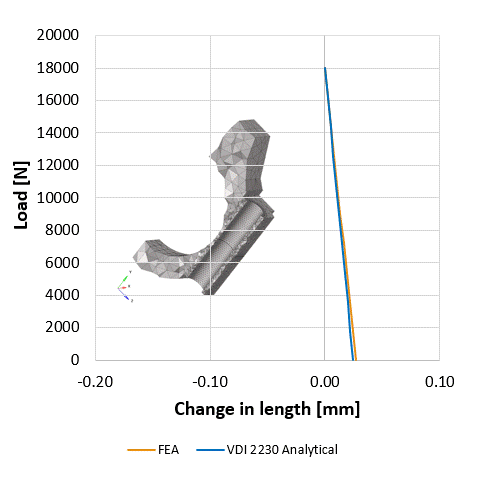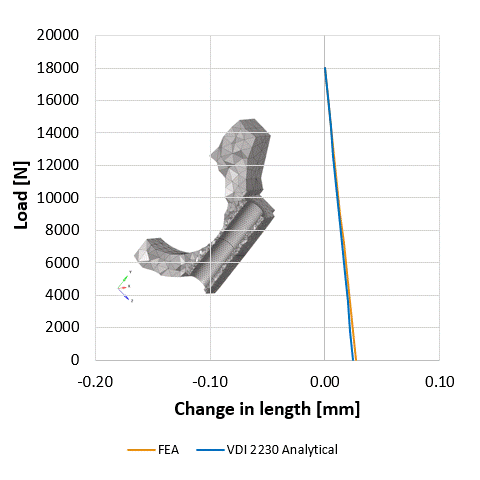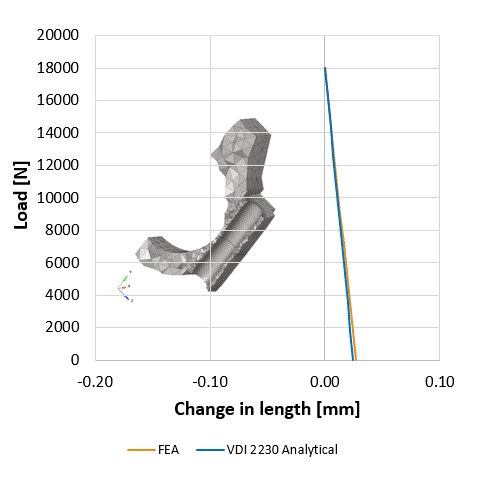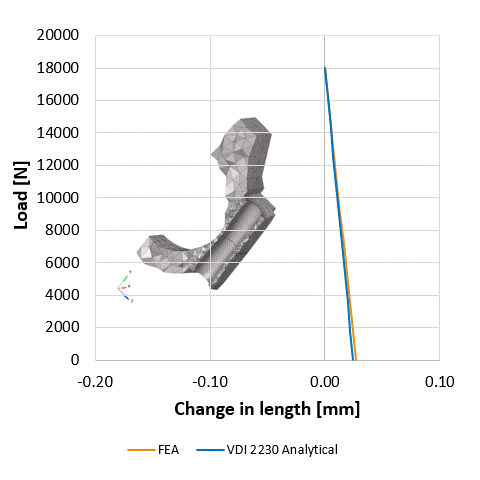
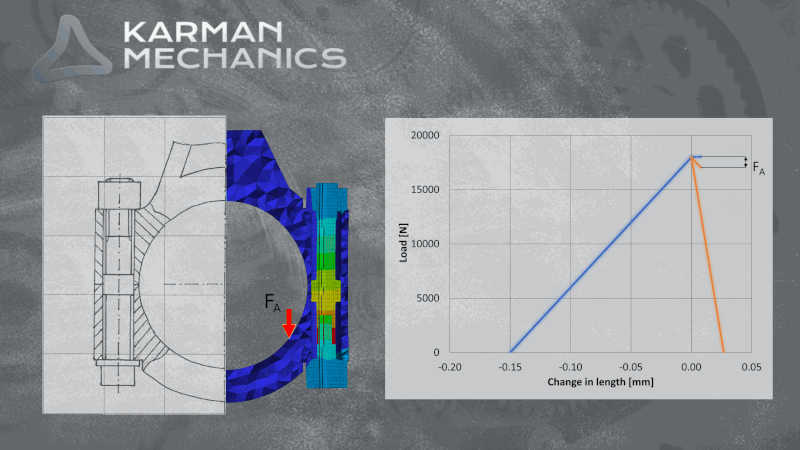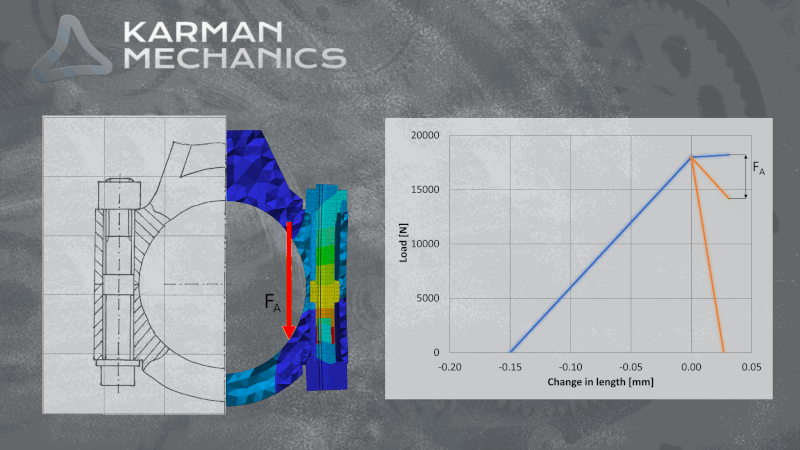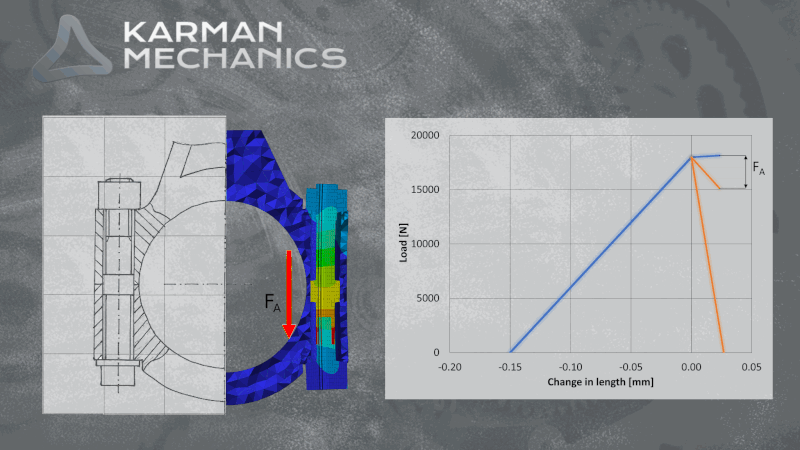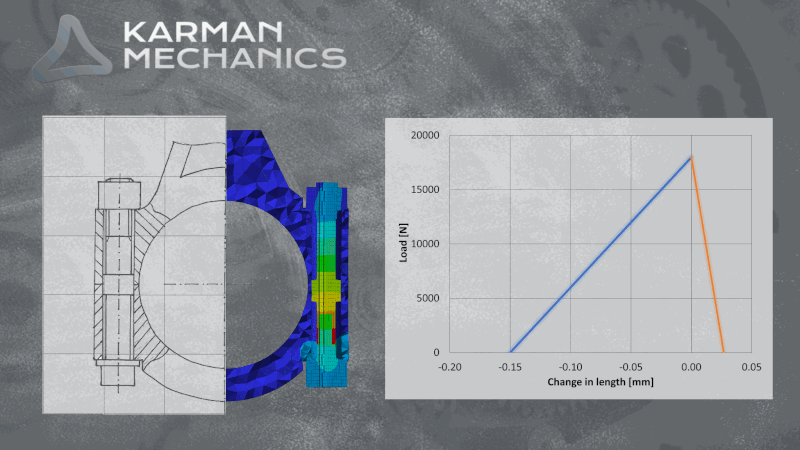
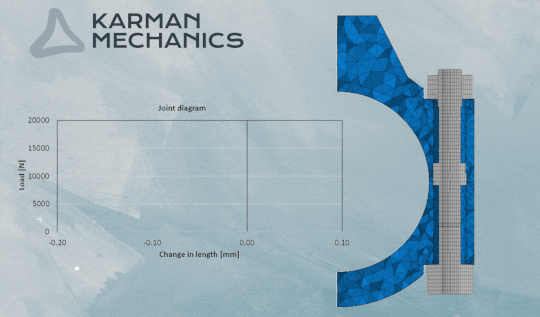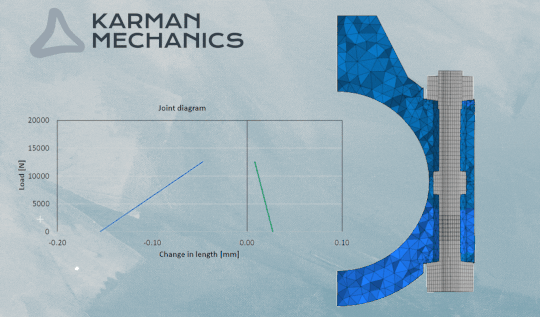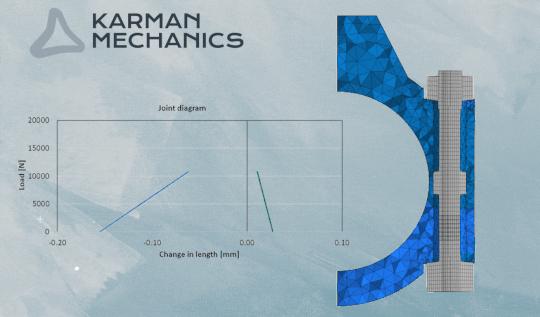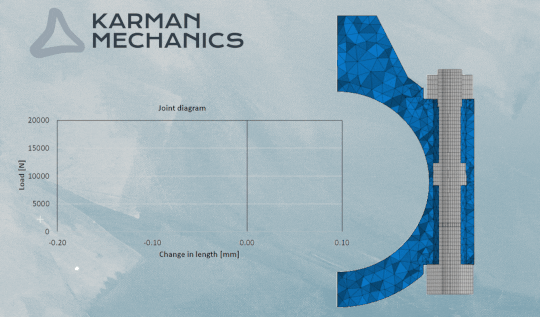
A sátordiagram

A gépészet egyik legizgalmasabb ábrája. Egyszerre mutatja az összeszorított elemek zömülését és a csavar megnyúlását, úgy eltolva azokat a vízszintes tengelyen, hogy azok a maximális előfeszítésnél metsszék egymást. Feltételezve, hogy a külső terhelés hatására a csavar és az összeszorított elemek azonos arányban vesznek részt a terhelés viselésében, akkor amennyivel pluszban megnyúlik a csavar, annyival csökken az összeszorított elemek zömülése (mínuszban). Ezt a sátordiagramnak a csavar merevségét ábrázoló szárának meghosszabbításával lehet egyszerűen ábrázolni. A terhelés ciklikussága ismétlődő igénybevételt okoz. Belátható, hogy a csavar és az összeszorított elemek merevségének illetve engedékenységének pontos meghatározása alapvető fontosságú ahhoz, hogy a fárasztó igénybevétel hatását pontosan meg lehessen határozni a csavaron. Mivel a keresett amplitúdó, a teljes erőjátéknak csak egy kicsiny része, ezért a számítási paraméterek kicsiny változása is óriási hatással lehet a csavar üzemi szilárdságát tekintve. Végeselemes szimulációk esetén is az tapasztalható, hogy elegendő az iterációs lépésköz változtatása ahhoz, hogy ugyan azon a modellen más-más élettartamot határozzunk meg ugyan arra a csavarkötésre ugyan annál a modellnél és ugyan annál a terhelésnél. Ennek részben a súrlódás az oka, amiről itt olvashatsz. Komoly tapasztalatokkal kell tehát rendelkezni ahhoz, hogy megbízható analitikus és végeselemes csavarszámításokat legyünk képesek végrehajtani.
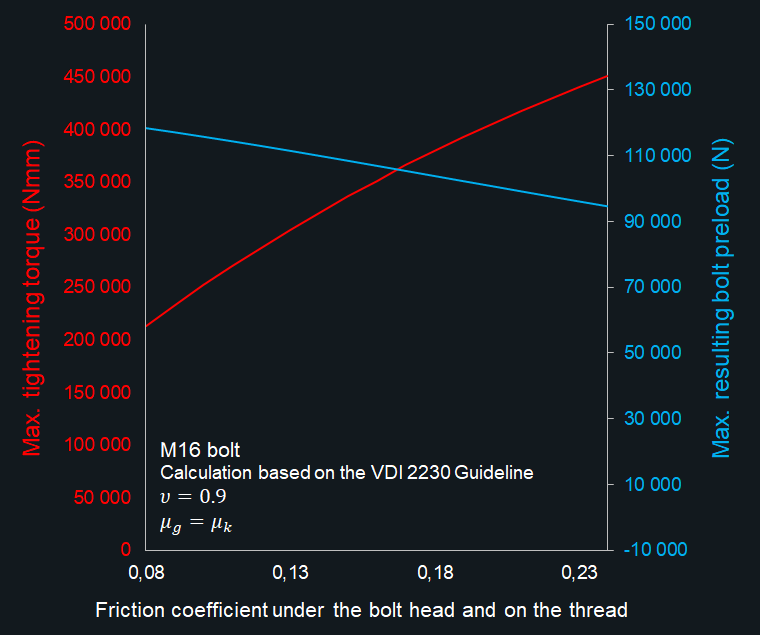
Súrlódás és csavarkötés

Erővel záródó kötés és épp emiatt kedveljük annyira, mert oldható, az élettartamán belül újra használható, robosztus, egyszerű a használata. Sajnos éppen az erővel záródás okozza egyben a legtöbb fejtörést is. Az erővel záródó kötések esetén a súrlódásból eredő erőnek kell biztosítania a kötés önzárását. A súrlódás viszont okozhat váratlan meglepetéseket a gyakorlatban. A súrlódás legkellemetlenebb jellemzője mérnöki szempontból az, hogy nem állandó az értéke. Tetézi a problémát, hogy a mérnöki gyakorlatban a Coulomb féle súrlódási modellel tudunk számolni, ami azt jelenti, hogy a csavarkötés megcsúszásának számításakor a megcsúszás mértékét nem tudjuk egzakt módon megadni. Csak azt tudjuk megbecsülni, hogy mekkora elmozdulás-tartományon belül áll meg valahol a csúszás. Ráadásul a tartomány mérete a súrlódási tényezőtől függ. Minél nagyobb a súrlódási tényező, annál szélesebb a tartomány tehát annál nagyobb szélsőértékekkel kell számolnunk. Kellemetlen lehet nagy súrlódási tényező esetén a szélső határhelyzetű nyugvópont, mert ez jókora hajlításból eredő nyomatékot jelent a csavarfej- vagy az anya alatt. Lásd az ábrát. Ennek a hatását végeselemes számítással sem egyszerű meghatározni. Azonban a nagy súrlódás nem csak kellemetlen hajlító nyomatékot okozhat! A súrlódás miatt fellépő csavaró nyomaték mibenlétét a csavarokban a következő blogbejegyzés fogja taglalni.
Csavarkötések, bevezetés

Az egyik talán legegyszerűbb gépelem, működésének hátterét tekintve egy egyszerű lejtő. Nincs is talán olyan berendezés, amiben ne lenne megtalálható, mindenki használja. Tudományos tekintetben nincs még egy ilyen sokat kutatott kötéstípus, a gyakorló mérnök mégis csak becslésekkel képes előállni egy csavarkötés teljesítményének előrejelzésére. Ez annak köszönhető többek között például, hogy a végtelenségig lehetne sorolni a gyakorlatból vett, nem tankönyvi eseteket úgy, mint: folyáshatárig feszített csavarok, előfeszítés alumíniumban, festékrétegen felfekvő alátétek, stb… A csavarkötés szilárdságának elemzése közben egyszerre több paraméterrel kell zsonglőrködni, ezért nem mindig egyszerű kiismerni magunkat a vonatkozó szabványok és méretezési eljárások (pl. VDI2330) ajánlásai, valamint a gyakorlati alkalmazási tapasztalatok adatai között.
Nem minden esetben szükséges alkalmazni, de a végeselemes analízis itt is sokat segíthet meghatározni egy-egy csavarkötés terheléseit és megbecsülni annak üzembiztonságát.
A következő posztokban körüljárunk néhány csavarkötéssel kapcsolatos témakört és rávilágítunk fontos tényezőkre, amik -legtöbbünk tudta nélkül- meghatározzák egy adott kötésnek a viselkedését.
Karman vortex shedding

2021.06.11.
Laminar flow around a 2D cylinder – Kármán vortex shedding
Low Reynolds number flows around a cylinder is one of the most well-known, and most investigated cases in Computational Fluid Dynamics (CFD). It is probably due to the interesting phenomenon that can occur in this type of flow, the Karman vortex shredding.
Around Re 90-150 the fluid behind the cylinder starts to produce vortexes with periodically opposite orientations. The phenomenon became a great benchmark and validation case, considering the simplicity of the geometry combined with the complex behaviour of the flow.
The purpose of this study is to investigate the effect of different meshing methods on the solution accuracy.
The lift- (CL) and drag coefficients (CD) were investigated on a 2D cylinder using OpenFOAM. Since these are time dependent – oscillating values, an average was calculated for the drag- and a root mean square for the lift coefficient using the following formulas:
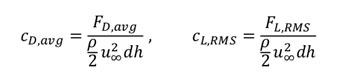
Flow with four different Re numbers (from 90-150) was examined. The investigations of Henderson and Norberg were considered as the target, the reference data is summarised in the table below.
Table 1. Experimental data for the cylindrical bodies

Air was used in the analyses, in order to accurately recreate the experimental environment. To maintain low Re numbers. we had to set our inlet velocity ranging from 0.0073 m/s to 0.022 m/s. The length of the wind tunnel was 10 meters, and the height was 8 meters. The model setup is displayed in the following sketch.

Figure 1. Model setup.
Since the simulation was laminar and transient, OpenFOAM’s icoFoam solver was used for the analysis. The initial mesh was generated with Salome Meca’s Netgen module. The prism-dominant (extruded triangles) mesh with the use of viscous sublayers consisted of 81 000 cells and can be seen in the pictures below.

Figure 2. CFD mesh generated by Salome Meca’s Netgen module consisting of 81 000 cells.
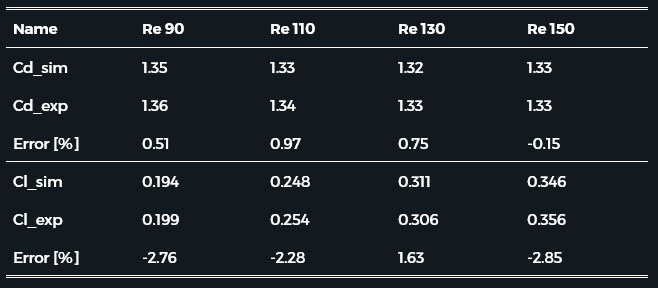
Table 2. summarises the simulation result lift- (CL) and drag coefficients (CD) compared with the experimental results. The simulation results seem accurate based on the comparison.
Table 2. Lift- and drag coefficient around a 2D cylinder at Re 90-150.
The following animation shows the laminar vortex shedding at Re = 150:
A further mesh convergence study was made, to find more efficient approaches to solve this problem.
Fully hexahedral meshes were investigated generated by OpenFOAM’s blockMesh utility. Four refinement levels were made, both with Salome and blockMesh. These meshes are displayed in the following Figures.
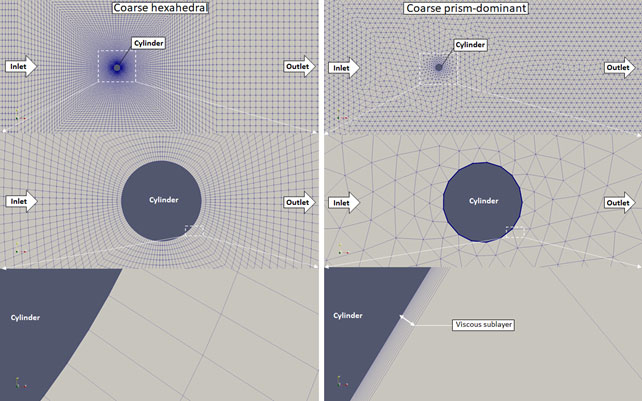
Figure 3. Coarse meshes generated with snappyHexMesh (left) and Salome Meca (right)
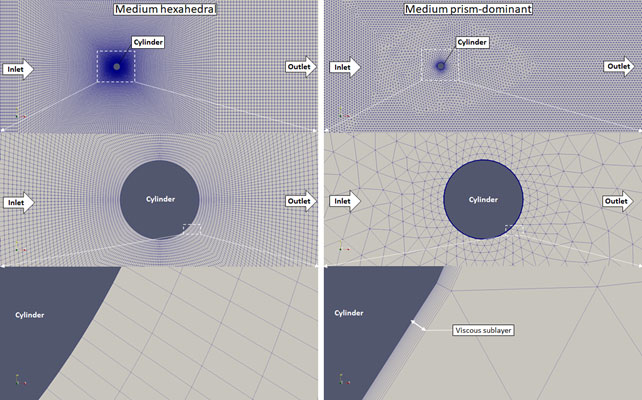
Figure 4. Medium meshes generated with snappyHexMesh (left) and Salome Meca (right)
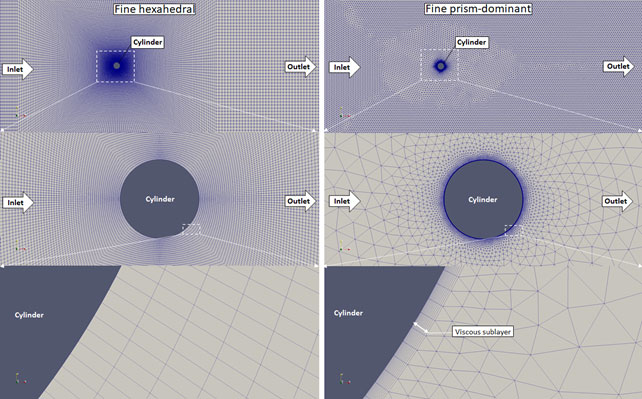
Figure 5. Fine meshes generated with snappyHexMesh (left) and Salome Meca (right)
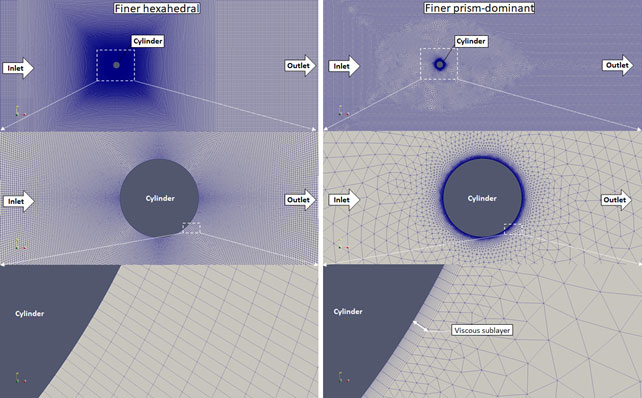
Figure 6. Finer meshes generated with snappyHexMesh (left) and Salome Meca (right)
The meshes displayed in Fig. 3-6. were used to run the scenario at a Reynolds number of 150. For these simulations the wind tunnel height was decreased to 3 meters, because it seemed to be perfectly enough for the flow to develop undisturbedly. The Salome generated meshes were labelled with “sm” initials whereas the blockMesh generated ones got the “bm” label.
An animation of the vortex shredding forming in each case.
And also diagrams of the lift- (CL) and drag coefficients (CD) in each timestep, on the coarse and finer prism-mesh.
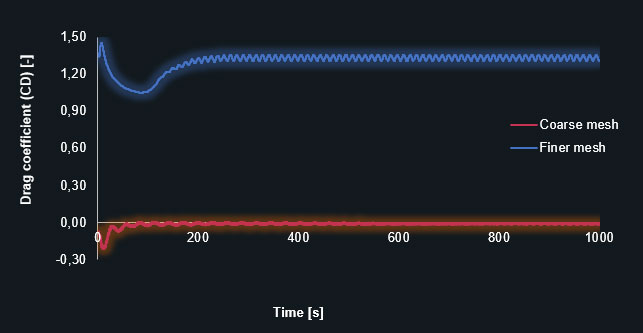
Drag coefficient (CL) in a coarse and finer prism-dominant mesh
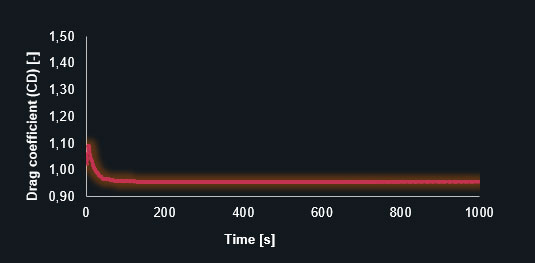
Drag coefficient (CD) – coarse prism-dominant mesh
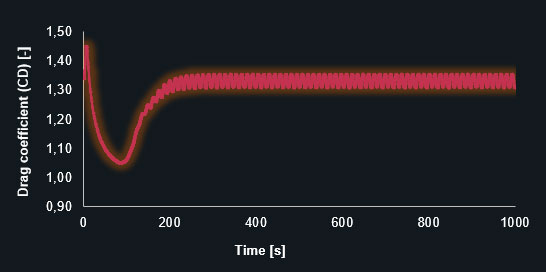
Drag coefficient (CD) – fine prism-dominant mesh
Lift coefficient (CL) – coarse prism-dominant mesh
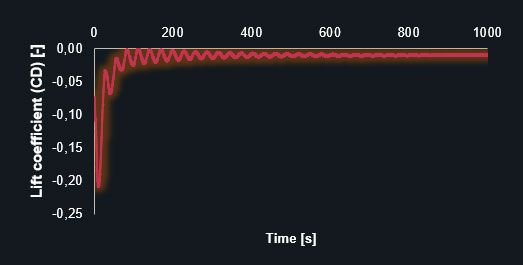
Lift coefficient (CL) – fine prism-dominant mesh
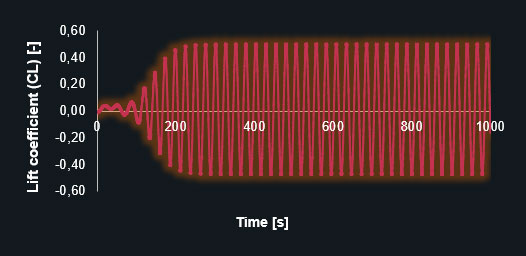
The diagrams clearly show that the finer mesh produces the expected oscillating results for the lift and drag coefficients. The simulation with the coarse mesh converges to a discrete value leading to an inaccurate solution. The following table contains the results in detail.
Table 3. Comparison of the different meshing methods at different refinement levels
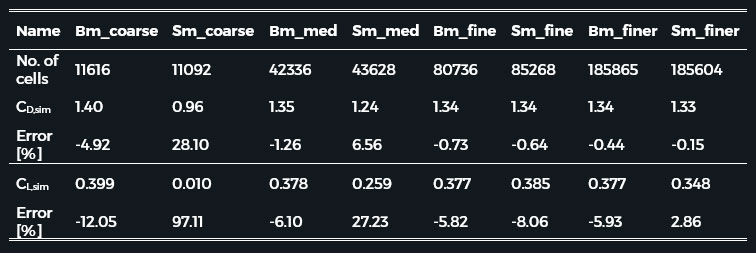
As the results show the hexahedral mesh can produce more accurate results with the same number of cells. But nevertheless, at the end, the Salome prism-dominant mesh gave the best result. This is probably due to the added viscous sublayers and the considerably finer mesh around the cylinder.
The animation also shows that the prism meshes that converged, converged much faster than the hexahedral ones. (Although the simulation with the coarse mesh didn’t even started the vortex shedding.)
Generally speaking, a blockMesh generated mesh leads to precise and fast results. In case one needs even more precision, it is worth using a finer mesh and viscous sublayers.






