Új végeselemes szoftverekkel történő ismerkedés során előre definiált számítási feladatok elvégzése a validáció egyszerű eszköze. Jelen bejegyzés összefoglal egy ilyen validációs folyamatot, mely egy nyílt forráskódú végeselemes környezetnek, a code_aster-nek (Salome Meca-n keresztüli futtatás) a vizsgálatára irányul.
A mintapélda (The Standard NAFMES Benchmarks: Hemisphere – Point Load, NAFEMS Ltd.) egy 10 [m] sugarú középfelületű, 0.04 [m] falvastagságú gömbhéjat vizsgál, mely egyidejűleg van húzásnak és nyomásnak kitéve (1. ábra). A terhelések 2 [kN]-os koncentrált erőkként kerülnek felvételre az 1. ábra szerint. A peremfeltételek és a geometria szimmetriáját kihasználva negyedmodell alkalmazható a jelenség vizsgálatára.
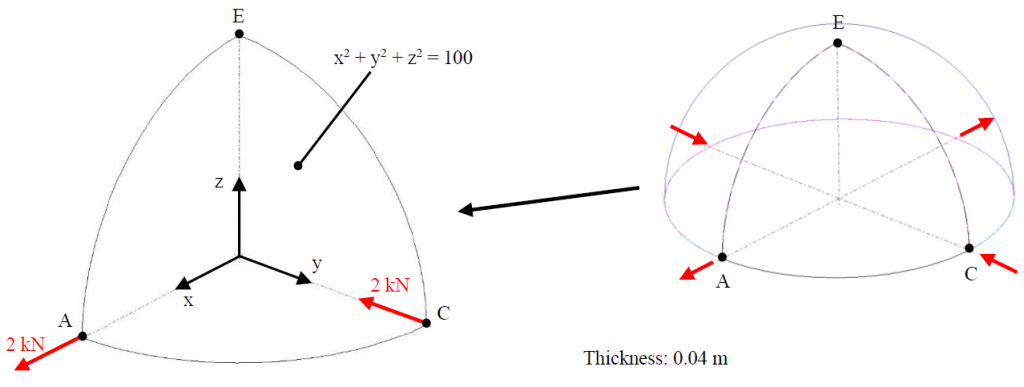
1. ábra – a feladat és a modell.
Morley és Morris elmélete (Morley, L.S.D., Morris, A.J. – Conflict Between Finite Elements and Shell Theory, Kiadvány: 2nd World Congress on Finite Elements: Finite Elements in the Commercial Environment, 532-561. oldal, 1978.) szerint az alábbi, membrán effektust, hajlítást és az élek hatását is figyelembe vevő összefüggéssel írható le a sugár irányú elmozdulás:
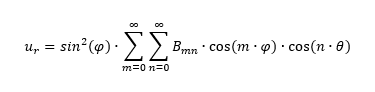
ahol θ a függőleges tengely körüli elfordulást, φ pedig a félgömb tengelyéhez képest sugárirányban mért szög. A Bmn-ek konstansok. Az adott paraméterek mellett az A pont sugár irányú elmozdulása:
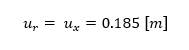
mely megadja a referencia értéket.
A terhelések mellett egyéb peremfeltételek definiálása is szükséges. Az E pont z irányú elmozdulása nulla, illetve szimmetria peremfeltételek hatnak az AE és CE éleken. Az alkalmazott anyagmodell izotropikus, E = 68.25∙103 [MPa], ν = 0.3 [-]. Héjelemek kerültek definiálásra a számításhoz.
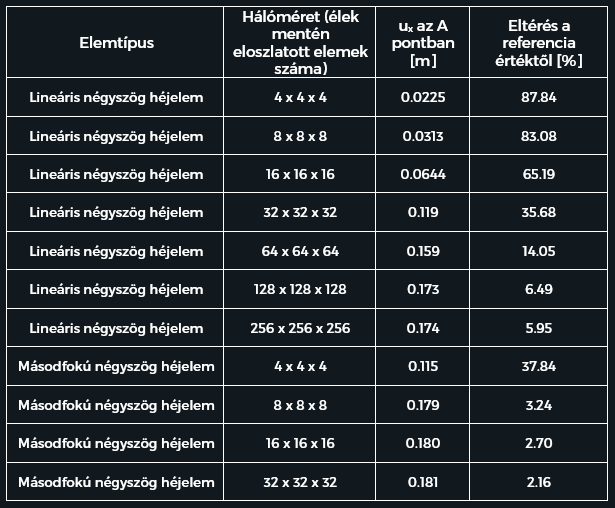
Az 1. táblázat összefoglalja a különböző elemméretű hálókkal készült számítások eredményeit. A hálóméret az egyes élek mentén egyenletesen eloszlatott elemek számát jelenti. Egy elmozdulás mező látható a 2 ábrán.
1. táblázat – a számítási eredmények.
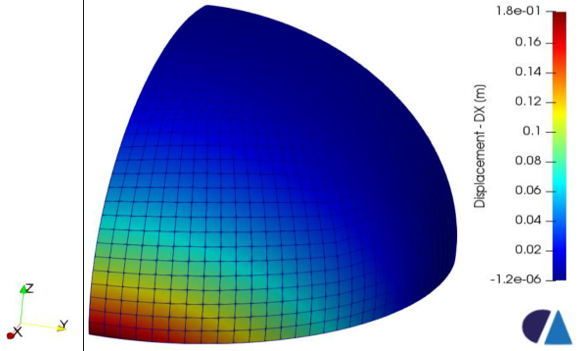
2. ábra – x irányú elmozdulás mező (másodfokú négyszög héjelem, 32 x 32 x 32).
A következő animáció összefoglalja a feladat alapvető információit, valamint a deformált alakkal kibővített elmozdulásmezőt.
A fent részletezett folyamat egy kitűnő lehetőség a nyílt forráskódú megoldások lehetőségeinek kutatására. Amennyiben erőfeszítéseink sikerrel zárulnak, lehetőségünk nyílik olcsóbb, de nem kevésbé szakszerű megoldásokat kínálni partnereink számára.







